Esplorare l’universo matematico: connessioni e contraddizioni
Le abilità scientifiche e matematiche sono ampiamente celebrate come chiavi del progresso economico e tecnologico, ma la matematica astratta può sembrare sconcertantemente lontana dall’ottimizzazione industriale o dall’imaging medico. La matematica pura spesso produce applicazioni impreviste, ma senza una macchina del tempo per guardare al futuro, come fanno i matematici a scegliere cosa studiare?
Durante i noodles tailandesi, è stato chiesto ad alcuni matematici cosa rende interessante un problema e hanno offerto una serie di suggerimenti: sorprese, contraddizioni, schemi, eccezioni, casi speciali, connessioni. Queste risposte potrebbero sembrare abbastanza diverse, ma supportano tutte una visione dell’universo matematico come struttura da esplorare.
In questa prospettiva, i matematici sono come anatomisti che imparano come funziona un corpo, o navigatori che tracciano nuove acque. Le domande che ci poniamo assumono molte forme, ma le più interessanti sono quelle che ci aiutano a vedere più chiaramente il quadro generale.
Fare mappe
Gli oggetti matematici si presentano in molte forme. Alcuni di loro sono probabilmente abbastanza familiari, come numeri e forme. Altri potrebbero sembrare più esotici, come equazioni, funzioni e simmetrie.
Invece di limitarsi a nominare gli oggetti, un matematico potrebbe chiedere come è organizzata una classe di oggetti. Prendiamo i numeri primi: sappiamo che ce ne sono infiniti, ma abbiamo bisogno di una comprensione strutturale per capire con quale frequenza si verificano o per identificarli in modo efficiente.
Altre buone domande esplorano le relazioni tra oggetti apparentemente diversi. Ad esempio, le forme hanno simmetria, ma anche le soluzioni di alcune equazioni.
Classificare gli oggetti e trovare connessioni tra di loro ci aiuta ad assemblare una mappa coerente del mondo matematico. Lungo la strada, a volte incontriamo esempi sorprendenti che sfidano gli schemi che abbiamo dedotto.
Tali apparenti contraddizioni rivelano dove la nostra comprensione è ancora carente e la loro risoluzione fornisce preziose informazioni.
Considera il triangolo
L’umile triangolo fornisce un famoso esempio di apparente contraddizione. La maggior parte delle persone pensa a un triangolo come alla forma formata da tre segmenti di linea di collegamento, e questo funziona bene per la geometria che possiamo disegnare su un foglio di carta.
Tuttavia, questa nozione di triangolo è limitata. Su una superficie senza linee rette, come una sfera o una foglia di cavolo riccio, abbiamo bisogno di una definizione più flessibile.
Quindi, per estendere la geometria a superfici che non sono piatte, un matematico dalla mentalità aperta potrebbe proporre una nuova definizione di triangolo: scegliere tre punti e collegare ciascuna coppia tramite il percorso più breve tra di loro.
Questa è una grande generalizzazione perché corrisponde alla definizione familiare nell’ambiente familiare, ma apre anche un nuovo terreno. Quando i matematici studiarono per la prima volta questi triangoli generalizzati nel XIX secolo, risolsero un mistero millenario e rivoluzionarono la matematica.
Il problema del postulato delle parallele
Intorno al 300 a.C., il matematico greco Euclide scrisse un trattato sulla geometria planare intitolato Gli elementi. Questo lavoro ha presentato sia i principi fondamentali che i risultati che ne sono stati logicamente derivati.
Uno dei suoi principi, chiamato postulato delle parallele, equivale all’affermazione che la somma degli angoli in ogni triangolo è 180°. Questo è esattamente ciò che misurerai in ogni triangolo piatto, ma in seguito i matematici hanno discusso se il postulato delle parallele dovesse essere un principio fondamentale o solo una conseguenza degli altri presupposti fondamentali.
Questo enigma persistette fino al 1800, quando i matematici capirono perché una dimostrazione era rimasta così sfuggente: il postulato delle parallele è falso su alcune superfici.
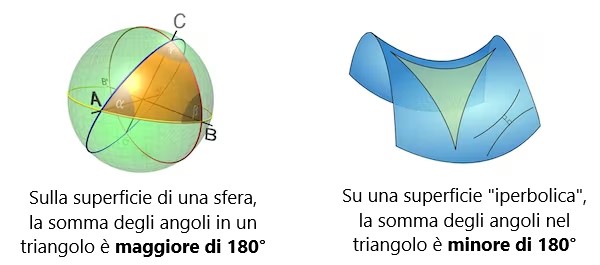
Su una sfera, i lati di un triangolo si piegano allontanandosi l’uno dall’altro e la somma degli angoli è superiore a 180°. Su una superficie iperbolica, i lati si piegano l’uno verso l’altro e la somma degli angoli è inferiore a 180°.
I triangoli in cui la somma degli angoli infrange la regola apparente hanno portato alla rivelazione che esistono tipi di geometria che Euclide non avrebbe mai immaginato. Questa è una verità profonda, con applicazioni in fisica, computer grafica, algoritmi veloci e oltre.
Anni verdi
Le persone a volte discutono se la matematica sia stata scoperta o inventata, ma entrambi i punti di vista sembrano reali per quelli di noi che studiano matematica per vivere. I triangoli su una superficie iperbolica sono sottili indipendentemente dal fatto che li notiamo o meno, ma selezionare quali domande studiare è un’impresa creativa.
Domande interessanti sorgono dall’attrito tra i modelli che comprendiamo e le eccezioni che li sfidano. Il progresso arriva quando conciliamo apparenti contraddizioni che aprono la strada per identificarne di nuove.
Oggi comprendiamo bene la geometria delle superfici bidimensionali, quindi siamo attrezzati per metterci alla prova con domande simili su oggetti di dimensioni superiori.
Negli ultimi decenni abbiamo imparato che anche gli spazi tridimensionali hanno le loro geometrie innate. La più interessante si chiama geometria iperbolica, e risulta agire come una versione tridimensionale del cavolo riccio. Sappiamo che questa geometria esiste, ma rimane misteriosa: nel mio campo di ricerca, ci sono molte domande a cui possiamo rispondere per qualsiasi spazio tridimensionale… eccetto quelle iperboliche.
Nelle dimensioni superiori abbiamo ancora più domande che risposte, ma è lecito affermare che lo studio della geometria quadridimensionale sta prendendo spazio tra gli studiosi.
Autore
Joan Licata, Australian National University