La vendetta di Pitagora: non sono stati gli uomini a inventare la matematica
Indice
La matematica, è quello di cui è fatto il mondo
Molte persone pensano che la matematica sia un’invenzione umana. Per questo modo di pensare, la matematica è come un linguaggio: può descrivere cose reali nel mondo, ma non “esiste” al di fuori della mente delle persone che la usano.
Ma la scuola di pensiero pitagorica nell’antica Grecia aveva una visione diversa. I suoi sostenitori credevano che la realtà fosse fondamentalmente matematica.
Più di 2000 anni dopo, filosofi e fisici stanno iniziando a prendere sul serio questa idea.
Come sostengo in un nuovo articolo, la matematica è una componente essenziale della natura che dà struttura al mondo fisico.
Api ed esagoni
Le api negli alveari producono nidi esagonali. Come mai?

Secondo la “congettura del nido d’ape” in matematica, gli esagoni sono la forma più efficiente per piastrellare un piano. Se si vuole rivestire completamente una superficie utilizzando piastrelle di forma e dimensione uniformi, mantenendo al minimo la lunghezza totale del perimetro, gli esagoni sono la forma da utilizzare.
Charles Darwin sosteneva che le api si sono evolute per utilizzare questa forma perché questa forma produce le celle più grandi per immagazzinare il miele per il più piccolo input di energia per produrre la cera.
La congettura del nido d’ape è stata proposta per la prima volta in tempi antichi, ma è stata dimostrata solo nel 1999 dal matematico Thomas Hales.
Cicale e numeri primi
Ecco un altro esempio. Esistono due sottospecie di cicale periodiche nordamericane che vivono la maggior parte della loro vita nel terreno. Poi, ogni 13 o 17 anni (a seconda della sottospecie), le cicale emergono in grandi sciami per un periodo di circa due settimane.
Perché 13 e 17 anni? Perché non 12 e 14? O 16 e 18?
Una spiegazione fa appello al fatto che 13 e 17 sono numeri primi.
Immagina che le cicale abbiano una serie di predatori che trascorrono anche la maggior parte della loro vita nel terreno. Le cicale hanno bisogno di uscire dal terreno quando i loro predatori sono dormienti.
Supponiamo che ci siano predatori con cicli di vita di 2, 3, 4, 5, 6, 7, 8 e 9 anni. Qual è il modo migliore per evitarli tutti?
Bene, confronta un ciclo di vita di 13 anni e un ciclo di vita di 12 anni. Quando una cicala con un ciclo vitale di 12 anni uscirà dal terreno, anche i predatori di 2, 3 e 4 anni usciranno dal terreno, perché 2, 3 e 4 si dividono equamente in 12.
Quando una cicala con un ciclo vitale di 13 anni esce dal terreno, nessuno dei suoi predatori uscirà dal terreno, perché nessuno dei 2, 3, 4, 5, 6, 7, 8 o 9 si divide equamente in 13. Lo stesso vale per 17.
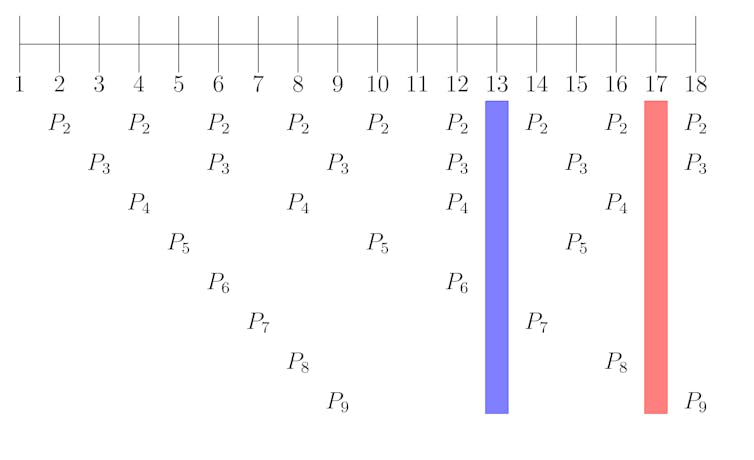
Le lacune evidenziate mostrano come le cicale di 13 e 17 anni riescano a evitare i loro predatori. Sam Baron, Autore fornito
Sembra che queste cicale si siano evolute per sfruttare i numeri.
Creazione o scoperta?
Una volta che iniziamo a cercare, è facile trovare altri esempi. Dalla forma delle bolle di sapone, al design degli ingranaggi nei motori, alla posizione e alle dimensioni degli spazi vuoti negli anelli di Saturno, la matematica è ovunque.
Se la matematica spiega così tante cose che vediamo intorno a noi, allora è improbabile che la matematica sia qualcosa che abbiamo creato. L’alternativa è che i fatti matematici vengano scoperti: non solo dagli esseri umani, ma da insetti, bolle di sapone, motori a combustione e pianeti.
Cosa ne pensava Platone?
Ma se stiamo scoprendo qualcosa, che cos’è?
L’antico filosofo greco Platone aveva una risposta. Pensava che la matematica descrivesse oggetti che esistono realmente.
Per Platone, questi oggetti includevano numeri e forme geometriche. Oggi potremmo aggiungere oggetti matematici più complicati come gruppi, categorie, funzioni, campi e anelli all’elenco.

Platone sosteneva anche che gli oggetti matematici esistono al di fuori dello spazio e del tempo. Ma una tale visione non fa che approfondire il mistero di come la matematica spieghi qualcosa.
La spiegazione implica mostrare come una cosa nel mondo dipende da un’altra. Se gli oggetti matematici esistono in un regno separato dal mondo in cui viviamo, non sembrano in grado di relazionarsi con nulla di fisico.
Entra nel pitagorismo
Gli antichi pitagorici concordavano con Platone che la matematica descrive un mondo di oggetti. Ma, a differenza di Platone, non pensavano che gli oggetti matematici esistessero al di là dello spazio e del tempo.
Invece, credevano che la realtà fisica fosse fatta di oggetti matematici nello stesso modo in cui la materia è fatta di atomi.
Se la realtà è fatta di oggetti matematici, è facile vedere come la matematica possa svolgere un ruolo nello spiegare il mondo che ci circonda.
Nell’ultimo decennio, due fisici hanno montato difese significative della posizione pitagorica: il cosmologo svedese-americano Max Tegmark e il fisico-filosofo australiano Jane McDonnell.
Tegmark sostiene che la realtà è solo un grande oggetto matematico. Se ti sembra strano, pensa all’idea che la realtà sia una simulazione. Una simulazione è un programma per computer, che è una specie di oggetto matematico.
La visione di McDonnell è più radicale. Pensa che la realtà sia fatta di oggetti e menti matematici. La matematica è il modo in cui l’Universo, che è cosciente, conosce se stesso.
Difendo una visione diversa: il mondo ha due parti, la matematica e la materia. La matematica dà alla materia la sua forma e la materia dà alla matematica la sua sostanza.
Gli oggetti matematici forniscono una struttura strutturale per il mondo fisico.
Il futuro della matematica
Ha senso che il pitagorismo venga riscoperto in fisica.
Nel secolo scorso la fisica è diventata sempre più matematica, rivolgendosi a campi di indagine apparentemente astratti come la teoria dei gruppi e la geometria differenziale nel tentativo di spiegare il mondo fisico.
Man mano che il confine tra fisica e matematica si offusca, diventa più difficile dire quali parti del mondo sono fisiche e quali matematiche.
Ma è strano che il pitagorismo sia stato trascurato dai filosofi per così tanto tempo.
Credo che stia per cambiare. È arrivato il momento di una rivoluzione pitagorica, che promette di alterare radicalmente la nostra comprensione della realtà.
Autore
Sam Baron, Associate professor, Australian Catholic University







